相关算法
第一章知识点
-
在数据结构中,从逻辑上可以把数据结构分为线性结构和非线性饥结构
-
与数据元素本身的形式、内容、相对位置、个数无关的是数据的逻辑结构
-
通常要求同一逻辑结构中的所有数据元素具有相同的特性,这意味着不仅数据元素所包含的数据项的个数相同,而且对应数据项的类型要一致
-
一些表面上很不相同的数据可以有相同的逻辑结构
-
算法的时间复杂度取决于问题的规模和待处理数据的初态
-
树数非线性数据结构
-
时间复杂度分为常数阶O(1);平方阶O(n^2);对数阶O(logn);开方阶O($$\sqrt{n}$$)
第二章知识点
-
在顺序表中插入元素的时间复杂度都是O(n^2),排序的时间复杂度为O(n^2)或者O(nlogn),顺序表访问节点直接通过数组的下标直接定位,时间复杂度是O(1)
-
向顺序表中插入一个新元素并保持原来顺序不变,平均要移动的元素个数是n/2
-
链接存储的存储结构所占存储空间分为两部分,一部分存放节点值,另一部分存放表示节点间关系的指针
-
线性表若采用链式存储结构,存储单元的地址连续或不连续都可以
-
线性表在需要不断的对其进行删除插入情况下使用链式存储结构合适
-
存储密度是值一个节点的数据本身所占的存储空间和整个节点所占的存储空间之比
-
将两个各有n个元素的有序表归并成一个有序表,最少的比较次数是n
-
单链表创建的时间复杂度是O(n), 而要创建一个有序的单链表时间复杂度是O(n^2)
-
链式存储结构和顺序存储结构各有优缺点,有不同的适用场合
-
单链表的插入过程
-
双向链表删除节点的过程
-
双向链表的插入过程
第三章栈与队列
-
进栈与出栈的次序问题(若1 2 3一依次进栈,不可能出现出栈的顺序为3 1 2)
-
计算队列中元素个数的方法和循环队列中元素个数的方法
-
删除链栈的栈顶节点过程
-
元素进栈的过程
-
栈在递归调用,函数调用, 表达式求值中有所应用
-
用链接方式存储的队列在删除运算时一般只需修改头指针,但是当删除的是队列中的最后一个元素时,队列指针也需要改变
-
循环队列入队的过程
-
循环队列队空与队列满的判断
第五章树和二叉树
-
把一棵树转换成二叉树后,这棵树的形态是唯一的
-
二叉树的相关性质(需进行一些计算)
-
二叉树的遍历: 前序遍历 中序遍历 后序遍历
-
完全二叉树的性质:度为0的节点个数 = 度为2的个数 + 1
-
二叉树节点数 = 度为0的节点个数 + 度为1的节点个数 + 度为2的节点个数
-
满二叉树的性质:第i层的节点个数为:2 ^(i - 1),总节点个数为2 ^ n - 1
-
二叉链表:左孩子右兄弟表示法,根节点的右指针为空
-
哈弗曼树没有度为1的节点
-
二叉线索树:加快查找节点的前驱和后继的速度
第六章图
-
关于图的一些概念:度 入度 出度 无向图 有向图等
-
无向完全图的性质:边的个数为n(n-1) / 2
-
有向完全图的性质:弧的个数为n(n-1)
-
有向图中所有顶点的入度之和等于所有顶点的出度之和
-
连通图前提是无向图 强连通图前提是有向图
-
深度优先遍历通常采用栈实现算法,广度优先遍历通常采用队列实现算法
-
深度优先遍历类似二叉树中的先序遍历
-
广度优先遍历类似二叉树中的层次遍历
-
图的邻接表算法
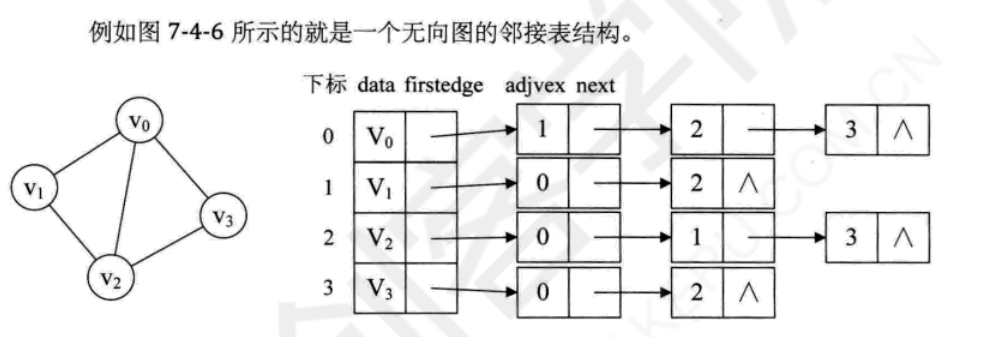
-
使用拓扑排序可以判断出一个有向图是否有环
第七章查找
-
适用于折半查找的表的存储方式以及排列要求为顺序方式存储,元素有序
-
折半查找的过程分析
-
如果要求一个线性表既能较快的查找,又能使用动态变化的要求,最好采用分块查找法
-
二叉排序树的过程分析
-
哈希查找:不存在特别好与坏的哈希函数,要视情况而定
-
采用链地址处理冲突时,查找一个元素的时间是不同的
第八章排序
-
几种排序的算法分析
-
希尔排序不能保证每趟排序至少能将一个元素放到其最终的位置上
-
仅要求求出某数据表中最大的10个元素堆排序最省时间




