0.3 + 0.6 竟然不等于 0.9???
场景分析
package main
import "fmt"
func main() {
var f1 float64 = 0.3
var f2 float64 = 0.6
var f float64 = f1 + f2
fmt.Println(f)
}

package main
import "fmt"
func main() {
var f1 float32 = 0.3
var f2 float32 = 0.6
var f float32 = f1 + f2
fmt.Println(f)
}

疑问点:为什么两种精度下的浮点数相加都不是0.9!
且听我细细说道。
计算机中整数的表示
首先我们要明确一点,计算机中只有0和1。这就是所谓的二进制。
不同于我们日常生活中的10进制,二进制即逢2进1。
那如何将10进制的数转换成2进制呢?以8421BCD码表示(8位)。
| 10进制(逢10进1) | 2进制(逢2进1)8421BCD码 |
|---|---|
| 0 | 0000 0000 |
| 1 | 0000 0001 |
| 2 | 0000 0010 |
| 3 | 0000 0011 |
| 4 | 0000 0100 |
| 5 | 0000 0101 |
| 6 | 0000 0110 |
| 7 | 0000 0111 |
| 8 | 0000 1000 |
| 9 | 0000 1001 |
| 10 | 0000 1010 |
以7为例子:7的二进制表示为0000 0111。
这样的表示其实是有问题的。因为还有负数,那计算机中该如何去表示负数呢?
聪明的计算机专家们使用了一个标志位来表示这个数是正数还是负数。即 0代表正数,1表示负数。
如7为正数,即0000 0111。
-7为负数,即1000 0111。
第一位为标志位,1只说明它是一个负数。
我们知道现在大多数计算机都是64位。
即7将表示为:
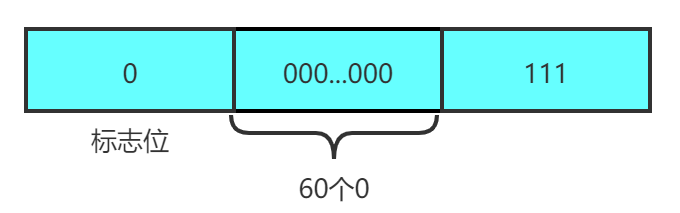
对于有符号的数来说,能表示的最大的数即为 ~
计算机中浮点数的表示
我们知道,计算机中不可能只有整数,那小数该如何表示呢?
如0.3等,其实是计算机中无法准确的表示0.3,只能近似表示。
| 2进制浮点数 | 10进制浮点数 |
|---|---|
| 0.000 | 0 |
| 0.001 | |
| 0.010 | |
| 0.011 | |
| 0.100 | |
| 0.101 | |
| 0.110 | |
| 0.111 |
我们尝试来表示一下0.3。
首先0.3接近于0.25。
| 2进制浮点数 | 10进制浮点数 |
|---|---|
| 0.010 | 0.25 小了 |
| 0.0101 | 大了 |
| 0.01001 | 小了 |
| 0.010011 | 小了 |
| 0.0100111 | 比较接近 |
我们将慢慢无限接近于0.3,但始终无法等于0.3。
如下用Go程序表示的结果,让小数点保留至20位。
其中float32最终结果为0.30000001192092895508。
float64最终结果为0.29999999999999998890。
package main
import "fmt"
func main() {
var f1 float32 = 0.3
var f2 float64 = 0.3
fmt.Printf("%.20f", f1) //0.30000001192092895508
fmt.Printf("%.20f", f2) //0.29999999999999998890
}
拿32位的单精度举例子:如下图。
这种表示法为计算机中的IEEE标准:用科学计数法表示。其中定义了两种基本格式:
-
32位表示单精度的浮点数,即我们常说的float32(golang),float(c) -
64位表示双精度的浮点数,即我们常说的float64(golang),double(c)
32位浮点数中各位的表示如下图:

-
第一部分:符号位1位,用来表示是正数还是负数。用s表示。 -
第二部分:指数位8位,我们一般用 e 来表示。8 个比特能够表示的整数空间,就是 0~255。我们在这里用 1~254 映射到 -126~127 这 254 个有正有负的数上。因为我们的浮点数,不仅仅想要表示很大的数,还希望能够表示很小的数,所以指数位也会有负数。 -
第三部分,是一个 23 个比特组成的有效数位。我们用 f 来表示。
综合科学计数法,我们的浮点数就可以表示成下面这样:
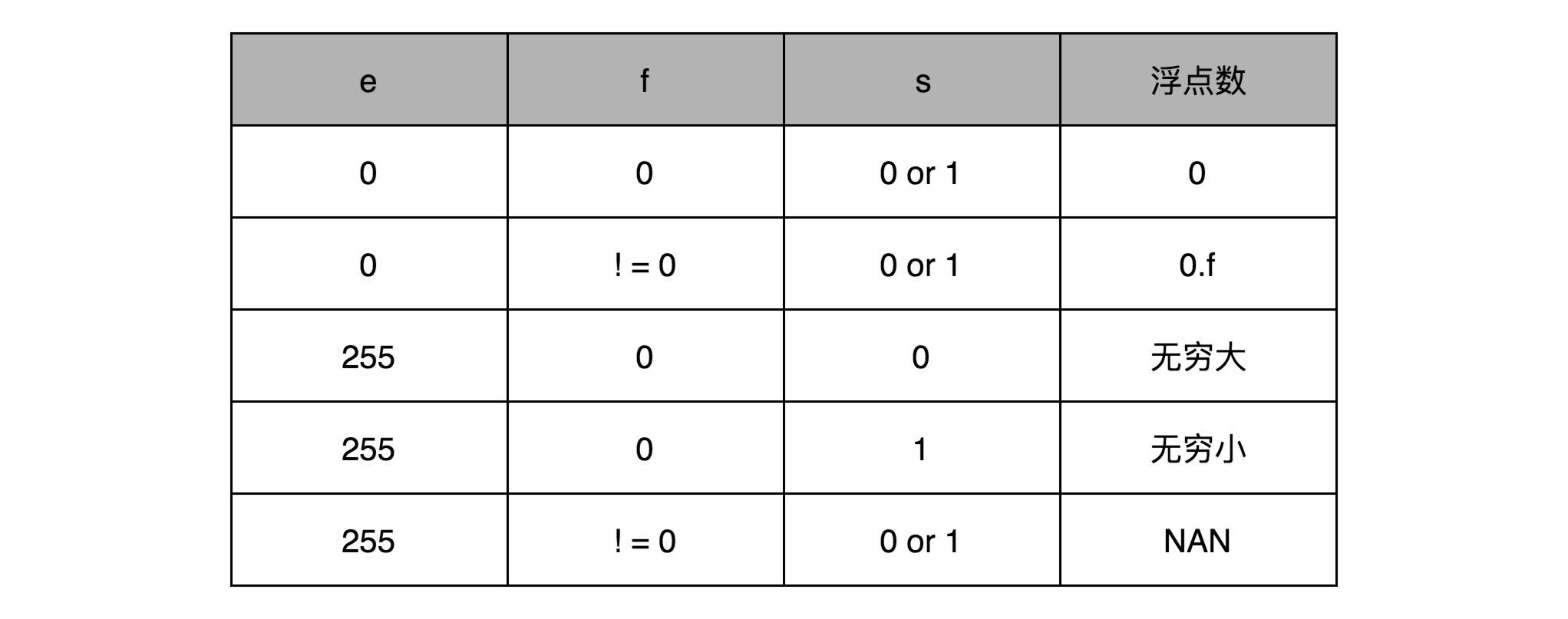
你会发现,这里的浮点数,没有办法表示 0。的确,要表示 0 和一些特殊的数,我们就要用上在 e 里面留下的 0 和 255 这两个表示,这两个表示其实是两个标记位。在 e 为 0 且 f 为 0 的时候,我们就把这个浮点数认为是 0。至于其它的 e 是 0 或者 255 的特殊情况,你可以看下面这个表格,分别可以表示出无穷大、无穷小、NAN 以及一个特殊的不规范数。
我们可以以 0.5 为例子。0.5 的符号为 s 应该是 0,f 应该是 0,而 e 应该是 -1,也就是,对应的浮点数表示,就是 32 个比特。

s=0,e=,需要注意,e 表示从 -126 到 127 个,-1 是其中的第 126 个数,这里的 e 如果用整数表示,就是 26+25+24+23+22+21=126,1.f=1.0。
分析开头的问题
我们知道了计算机中是如何表示浮点数之后,那么0.3+0.6 != 0.9的问题就迎刃而解了。
公式:
我们找不到对应的s,f,e的值满足上述式子。只能无限逼近0.3。
0.6也是一样,所以两者相加也得不到0.9了。
那0.5与0.375是可以的哦,尝试一下!
package main
import "fmt"
func main() {
var f1 float32 = 0.5
fmt.Printf("%.50f\n", f1)
var f2 float32 = 0.375
fmt.Printf("%.50f\n", f2)
var f float32 = f1 + f2
fmt.Printf("%.50f\n", f)
}